Ballpark Similarity Scores
Written by John Incantalupo
Introduction
In the mid-1980s, legendary baseball statistician Bill James introduced the player similarity score, a statistic that aimed to compare two players’ careers to one another by calculating differences in their career counting stats. I have always loved looking through the similarity scores on a player’s Baseball Reference page, and I thought it would be interesting to apply this concept to MLB stadiums. Unlike most other sports, the field of play in baseball differs from place to place. Although there are many specifications that all MLB ballparks must follow, such as 60 feet, 6 inches from home plate to the pitcher’s mound and 90 feet between bases, stadium constructors are given a lot of freedom in many other aspects when designing a baseball field. The varying dimensions of these ballparks are what give baseball one of its many unique quirks, especially when something happens during a game that would only occur in that particular ballpark. Even though major strides have been made in recent years to quantify these differences, such as the creation of park factors, they have mostly been used to create neutralized statistics for individual players rather than comparing the ballparks themselves.
So, I decided to create a statistic based on James’ player similarity score that measured the similarity between two ballparks. The initial goal was to use this score to compare Major League ballparks to one another, but I also wanted to expand this project to include affiliated minor league ballparks, ranging from Single-A to AAA. In total, I compiled data from 149 different ballparks in an effort to create a similarity score statistic. The data was taken from the 2022-2024 seasons, meaning that newly opened ballparks such as Daybreak Field in Salt Lake City, Utah, are excluded from this project, while recently closed ballparks such as the Oakland Coliseum are included.
Collecting the Data
The data that I will be using to calculate this ballpark similarity score can be grouped into two categories: park factors and park dimensions. Park factors describe the run environment of a ballpark in a single number. There are six component park factors that will be contributing to this similarity score: strikeouts, walks, singles, doubles, triples, and home runs. Essentially, each component factor can be described as the rate at which each event occurs in that ballpark compared to the average ballpark, put on a scale where 100 is average. As an example, a home run park factor of 120 indicates that home runs occur 20% more frequently at that ballpark compared to the average ballpark in that league.
There are many ways that one can compute park factors, but I ended up using this method proposed by Jim Furtado. Although there are many sites such as Baseball Savant and FanGraphs that provide robust park factor calculations for all 30 MLB ballparks, I noticed that none of these sites also provide park factors for the minor leagues. I wanted to make sure that the same method was used in the calculations of both MLB and MiLB ballparks in order for their park factors to be comparable to one another, so I ended up just manually calculating these park factors myself using Furtado’s method. For this, I used play-by-play data scraped from MLB Gameday from the 2022-2024 seasons. I wanted to pull from a large sample, and there were no new home ballparks that opened during this time frame. As a result, the park factors used may be slightly different from the ones that you would see on a site like FanGraphs or Baseball Savant.
On the other hand, park dimensions are the physical measurements of a ballpark. Most of the dimensions that I used are the measurements of a ballpark’s outfield. These consist of outfield distances from home plate to left, left-center, center, right-center, and right fields, as well as fence heights for left, center, and right fields, all measured in feet. I also decided to incorporate the total area of the field in fair territory, measured in thousands of square feet, and the elevation of the ballpark, measured in feet above sea level. The dimensions for the 30 MLB ballparks were easy to obtain, thanks to Andrew G. Clem’s baseball blog. However, gathering data for the minor league ballparks was a lot more difficult given the lesser amount of public data available. Thankfully, the people in the Out of the Park Baseball community were a major help, as I found a forum page that had compiled the park dimensions for most MiLB ballparks. Although I still had to manually measure the dimensions for some of the newer and recently affiliated ballparks using Google Earth, that community post was still a massive help in making sure that the data collection phase didn’t take forever. Also, given the wide variety of sources used to gather the MiLB park dimensions, please note that some of these dimensions may not be 100% accurate.
Constructing the Formula
Now that all the data needed had been acquired, I began constructing the formula for this similarity score. After researching methods for measuring similarity between two observations, I settled on using Euclidean distance due to its relative simplicity compared to other methods. Now, if math is not your thing and you’re just looking for the results, then feel free to skip to the Calculating the Results section below.
Euclidean distance measures the proximity of two vectors. It is most commonly used in a 2D space, where it is based on the Pythagorean Theorem. This is the application of the Euclidean distance that most people are familiar with. However, the Euclidean distance formula can be extrapolated to vectors of higher dimensions. If we have two vectors of length n, {x1, x2, …, xn} and {y1, y2, …, yn}, then the formula for calculating Euclidean distance is as follows:
Since we are finding the squared difference between variables, a larger difference in variables will result in a higher number. Therefore, a lower similarity score will indicate that the pair of ballparks is more similar than others.
Before I threw all of the variables mentioned above into this Euclidean distance formula, there were a few adjustments that needed to be made. First, you might have noticed that not all variables are on the same numeric scale. The outfield distances of these ballparks range from 300 to over 400 feet, while the tallest outfield fences in this study top out at “just” 37 feet. Therefore, a 10-foot difference in left field fence height is a lot more significant than a 10-foot difference in left field distance. So, I standardized each variable so that they are all on the same scale.
Once the data has been standardized, each variable will now be weighted equally when put into the Euclidean distance formula. However, I do think that some of the variables should have a larger weight in the formula. So, I ended up splitting the variables into three groups, where I calculated the Euclidean distance of each group separately before applying a weight. The first group is comprised of the six park factors, the second group contains the outfield distances and fence heights, and the last group is the fair territory area and elevation. I did not want the outfield park dimensions to be weighed the same as the fair territory area and elevation variables, which is why those two variables were grouped into a separate category. I will be referring to this group as ‘miscellaneous.’ After experimenting with a variety of different weights, I eventually decided on 60% park factors, 30% park dimensions, and 10% miscellaneous. Park factors being weighed twice as much as park dimensions may seem a little extreme, but it is important to note that each group does not have the same number of variables. Groups with more variables, such as the park dimensions group, tend to create a larger Euclidean distance on average. Therefore, the difference in weights between park factors and park dimensions is not as extreme as it may initially seem.
The final similarity score formula is listed below:
One final thing to note before we jump into the results. The Palm Beach Cardinals and the Jupiter Hammerheads, the Low-A affiliates of the St. Louis Cardinals and Miami Marlins, respectively, had the unique distinction of being the only two minor league teams in 2024 to share a home venue, that being Roger Dean Chevrolet Stadium in Jupiter, Florida. When calculating the park factors for the minor leagues, I had to keep this in mind since I was grouping the data by home team. I ended up calculating two separate groups of park factors, one for the Cardinals’ home games and one for the Hammerheads’ home games, and took the average park factor for each component.
Calculating the Results
Now that the formula has been constructed, it is time to compare MLB ballparks! As mentioned in the previous section, this statistic operates on a reverse scale, where more similar pairs of ballparks will have lower similarity scores.
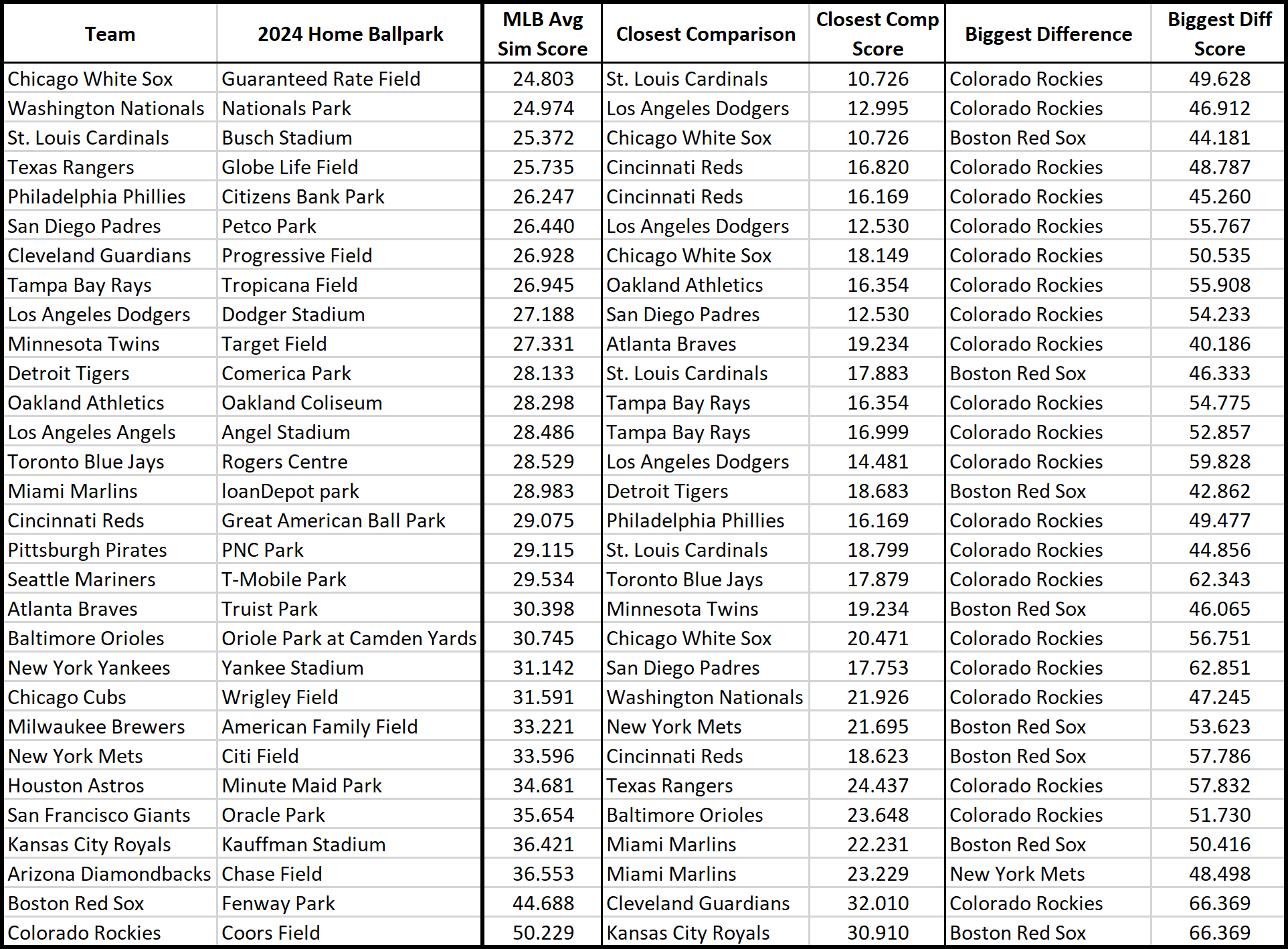
Here is the distribution of the similarity scores of all 435 unique pairings of MLB stadiums. There is a slight skew to the right, which can be attributed to one particular ballpark that was a clear outlier among the rest. Of course, I am talking about Denver’s Coors Field. This stadium, which has long been infamous for being a hitter’s paradise due to its high elevation and large outfield, accounted for 17 of the 20 highest similarity scores. Its elevation of 5,190 feet above sea level is nearly five times higher than the next closest, and its average park factor of 108 is also by far the highest among the 30 MLB stadiums. Coors’ largest similarity gap, which is also the largest similarity score in the sample, is with Boston’s Fenway Park. While Coors is an outlier in terms of park factors, Fenway is an outlier in terms of park dimensions. It boasts both the tallest outfield fence, the Green Monster, and the shortest outfield distance, the Pesky Pole in right field, in the entire Major Leagues. Therefore, it is no surprise that the combination of these two unique stadiums creates a mammoth similarity score of 66.369, the largest in this initial sample.
On the contrary, the two MLB ballparks that my formula deemed to be the most similar are St. Louis’ Busch Stadium and Chicago’s Rate Field, formerly Guaranteed Rate Field. This pairing finished with the lowest park factor score and the eighth-lowest park dimension score. There are no dimensions or park factors that make either of these two stadiums stand out, which may be why they scored the lowest. On average, these two ballparks differed by an average of 5 feet for the outfield distances and 2.3 for the park factors. Also, their outfields both have a uniform 8-foot fence, which further helps the park dimension score. Overall, Busch Stadium and Rate Field’s similarity score of 10.726 tops the entire field of 435 pairings.
Below is a heatmap displaying the similarity scores of all MLB stadium pairings, with a darker color signifying a lower similarity score. If you would like to know any of the exact similarity scores calculated, there is a CSV file detailing the Euclidean distance components of each pairing in the GitHub repository that I created for this project, which you can view here.
Next, I decided to calculate the average similarity score for each stadium, as well as their closest comparison and furthest difference. Unsurprisingly, Coors Field’s average similarity score of 50.229 was by far the highest among the 30 MLB stadiums. On the other hand, Rate Field had the lowest score on average with 24.803. Interestingly, 29 of the 30 MLB teams’ largest similarity score was with either Coors or Fenway. As mentioned before, each of these two ballparks was a massive outlier in one of the two major categories, so this makes sense.
As alluded to before, I also wanted to compare these 30 MLB stadiums to their minor league affiliates. By doing so, we can determine which organization’s ballparks are the most consistent throughout the minors. In this part, I created another statistic called Total Affiliate Score, or TAS, that seeks to calculate just that. Don’t worry, the TAS formula is not as complicated as the previous one. I just took each minor league ballpark’s similarity score with their MLB affiliate and added them up.
The first thing I noticed after calculating all 120 affiliate similarity scores is that the similarity scores between MLB stadiums and their minor league affiliates were on average higher than the similarity scores between two MLB stadiums. This may be due to the less consistent run environments and park dimensions of the minor league ballparks.
Now, I know you are all waiting to see where your favorite MLB team landed in the TAS rankings. But rather than simply describing some of the highlights of these rankings, I created graphics for each MLB organization sorted from largest TAS to smallest TAS, highlighting each component of their affiliates’ similarity scores. I have provided each affiliate’s similarity score with their MLB organization, as well as where their park factor, park dimension, and miscellaneous components ranked among ballparks at that level of the minors.
*Team changed stadiums prior to the 2025 season **Team relocated and changed names prior to the 2025 season All logos taken from SportsLogos.net.
Out of the 120 minor league affiliates, it was the West Michigan Whitecaps, the High-A affiliate of the Detroit Tigers, that posted the lowest similarity score. Their score of 12.793 would have ranked third among pairs of MLB stadiums, and is the main reason why the Tigers have the lowest TAS among MLB organizations. Meanwhile, the Albuquerque Isotopes of AAA had the highest similarity score, that being 78.595, when paired with their MLB affiliate, the Colorado Rockies. In fact, each of the Rockies’ four affiliates had a similarity score of over 70, which is higher than all 435 similarity scores between pairs of MLB stadiums. Although the Rockies once again finished with the largest value in these rankings, there was not much correlation between each organization’s average MLB similarity score and their total affiliate score, as shown in the scatterplot below. The team with the highest TAS besides the Rockies, the St. Louis Cardinals, had the third-lowest average similarity score between other MLB ballparks. Overall, the two variables had a correlation coefficient of 0.5584, signifying a relatively weak correlation.
What’s Next?
Although I am proud of the similarity score statistic that I came up with, it is still a work in progress. I want to add more components to this formula in the future, especially weather effects such as average temperature and precipitation. It would also be interesting to see if TAS has any correlation with how a team’s prospects progress through the minors. I would also like to hear from you all! If you have any suggestions that could improve upon this formula, let me know! This was my first independent research project, and I am quite happy with how this turned out. Thank you all for taking the time to read this, and stay tuned for more projects just like this one!
You can view my GitHub repository for this project here. This includes the R code used to calculate the similarity score statistic, as well as various CSV files that were used throughout the project.
Sources
About Player Similarity Scores